[LeetCode] Maximum Subarray

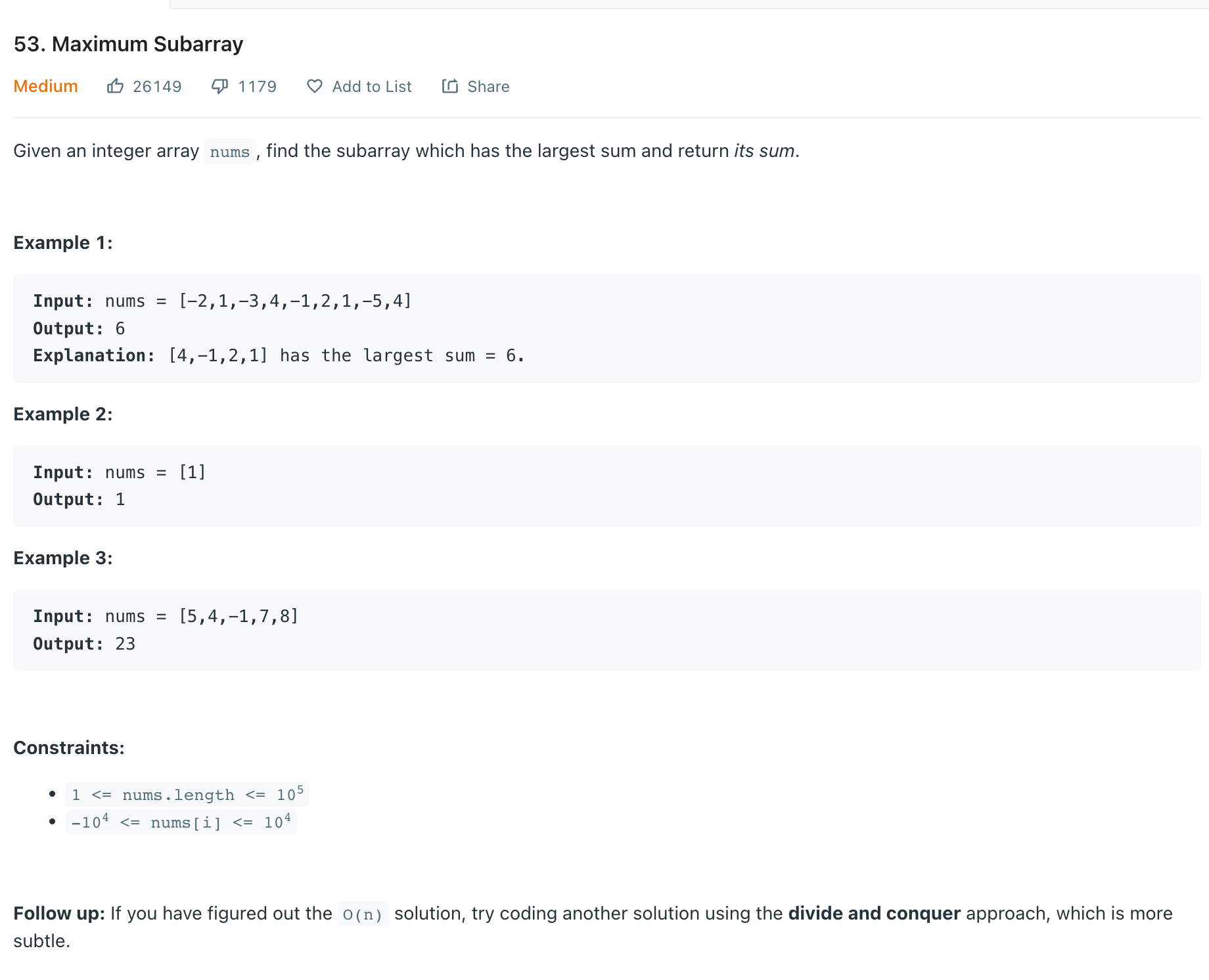
문제

첫 번째 접근: 완전탐색(Brute Force)

모든 subarray를 구해서 최댓값을 가지는 subarrayf를 구해보려했다.

하지만 시간초과가 났다. 데이터 크기가 10000이므로 O(N^2)에 해당하는 완탐은 시간 초과가 날 수 밖에 없다.

class Solution {
    public int maxSubArray(int[] nums) {
    
        int answer = Integer.MIN_VALUE;
        
        for (int s=0; s<nums.length; s++) {
            int e = s;
            int sum = 0;
            while(e<nums.length) {
                
                sum += nums[e];
                answer = Math.max(answer, sum);
                e++;
            }
        }
        return answer;
    }
}

두 번째 접근: DP(동적계획법)

동적계획법은 분할정복과 유사하다. 큰 문제를 풀기 위해 작은 문제를 푼 다음에 큰 문제의 답을 구한다.

여기서 작은 문제의 답을 저장했다가 더 큰 문제를 풀기 위해 작은 문제를 이용한다. 즉 동적계획법은 큰 문제 형식과 작은 문제 형식이 재귀적으로 연결되어있다.

 

dp[i]는 nums[i]로 끝나는 subarray의 최댓값이라고 하자.

그러면 DP 형식으로 식을 작성한다면 다음과 같이 작성할 수 있다.

maxSubArr(A,i) = A[i] + (maxSubArr(A, i-1) > 0 ? maxSubArr(A, i-1) : 0)

dp[i] = nums[i] + (dp[i-1] > 0 ? dp[i-1] : 0)

즉 더 작은 문제 dp[i-1]로 dp[i]를 구할 수 있고 결국 전체 배열에서 subarray의 최댓값을 구할 수 있다.

 

이 경우 시간복잡도는 배열을 한 번만 순회하므로 O(N)이다.

class Solution {
    public int maxSubArray(int[] nums) {
        int n = nums.length;
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        int max = dp[0];
        
        for (int i=1; i<n; i++) {
            dp[i] = nums[i] + (dp[i-1] > 0 ? dp[i-1] : 0);
            max = Math.max(max, dp[i]);            
        }
        
        return max;
    }
}