Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 클라우드에서 도커 실행하기
- 인텔리제이
- String.valueOf()
- Spring Web MVC
- GCP
- vm인스턴스생성
- 프로그래머스
- 코드스테이츠
- 백준
- 알고리즘
- Array.asList
- 코딩테스트
- 재귀와반복문
- 코드스테이츠 백엔드
- List.of
- 성능테스트툴
- Spring MVC 동작원리
- Spring MVC 구성요소
- OOP
- 구간합구하기
- 버블정렬
- 투포인터알고리즘
- MySQL
- 스택
- 11659
- 자바
- java
- 백준 11659
- 싱글톤패턴
- 재귀함수
Archives
- Today
- Total
순간을 기록으로
[JAVA] 2018번 통계학 본문
https://www.acmicpc.net/problem/2108
2108번: 통계학
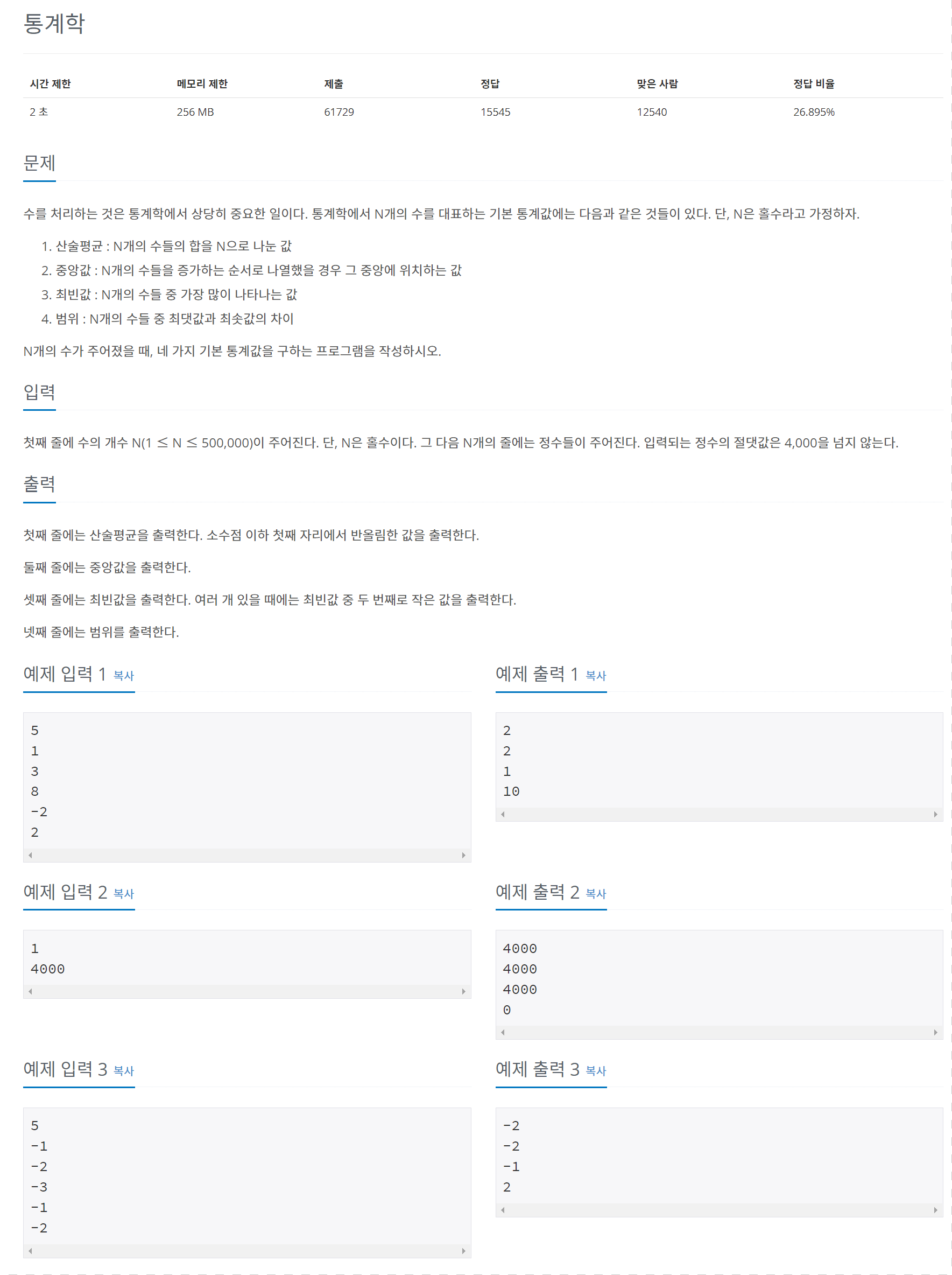
첫째 줄에 수의 개수 N(1 ≤ N ≤ 500,000)이 주어진다. 단, N은 홀수이다. 그 다음 N개의 줄에는 정수들이 주어진다. 입력되는 정수의 절댓값은 4,000을 넘지 않는다.
www.acmicpc.net
- 목표
- 평균 값을 구할 수 있다.
- 중앙값을 구할 수 있다.
- 최빈값을 구할 수 있다.
- 최댓값과 최솟값을 구할 수 있다.
푸는 순서: 1.문제 읽기 --> 2.수도코드 작성하기 --> 3.코드 작성하기 --> 4.테스트케이스 만들기.
맨 처음에 각 구하는 값을 함수 별로 담에서 구하려 했다. 하지만 생각보다 코드가 중복되는 걸 확인하고 함수로 분리하는 게 오히려 좋지 않을 수 있다는 생각이 들어 리팩토링 했다.
수도코드
- 수의 갯수 N를 입력받는다.(1<=N<=500,000, N은 홀수이다.)
- BufferedReader사용
- 다음 줄부터 N번 정수를 입력받는다.(입력받는 정수의 절댓값은 4,000을 넘지 않는다.)
- 평균값(N의 수들의 합을 N으로 나눈 값)을 구한다.
- 배열의 합을 구한다
- 배열의 길이를 구한다
- 평균값 = 배열의 합 / 배열의 길이
- 평균값은 소수 첫째자리에서 반올림한다.Math.round사용.
- 중앙값(N개의 수를 오름차순으로 나열 했을 때 중앙에 오는 값)을 구한다.
- Arrays.sort를 사용해서 배열을 오름차순으로 만든다.
- {1}에서 중앙값은 1이고 1의 인덱스는 0이다. 배열의 길이 / 2를 하면 0이 나온다.
- {1, 2, 3}에서 중앙값은 2이고 2의 인덱스는 1이다. 3(배열의 길이) / 2를 하면 1이 나온다.
- {1, 2, 3, 4, 5}에서 중앙값은 3이고 3의 인덱스는 2이다. 3의 인덱스는 5(배열의 길이) / 2를 하면 나온다.
- 중앙값은 배열의 길이 / 2를 이용해 중앙값의 인덱스를 구해 접근한다.
- 최빈값(N개의 수 중에서 가장 많이 등장한 값)을 구한다.
- value의 빈도수를 저장하는 count배열을 선언한다.
- 이때 count 배열의 길이는 될수 있는 값의 범위 이므로 8001으로 선언한다.
- count 배열에 빈도 값을 넣어준다.
- 최빈값은 count 배열의 최댓값이므로 count 배열의 최댓값을 찾는다.
- count 배열의 첫 원소값을 max로 잡고 순회한다.
- 단 최빈값이 여러 개 일 경우 두번 째로 작은 최빈 값을 출력해야되므로 flag(깃발)을 표시해 두 번째 인지 확인한다.
- 최댓값일 경우 해당하는 인덱스 - 4000을 최빈값 변수 mode에 넣는다.
- 범위(N개의 수들 중 최댓값과 최솟값의 차이)를 구한다.
- 위에서 Arrays.sort()할 때 최댓값을 구한다.
- 위에서 Arrays.sort()할 때 최솟값을 구한다.
- 범위 = 최댓값 - 최솟값
- 평균값을 출력한다.
- 중앙값을 출력한다.
- 최빈값을 출력한다.(최빈값이 여러 개 있을 경우 두 번째로 작은 값을 출력한다.)
- 범위를 출력한다.
package 백준.정렬.통계학_2108;
/*
* 목표
* 1.평균 값을 구할 수 있다.
* 2.중앙 값을 구할 수 있다.
* 3.최빈 값을 구할 수 있다.
* 4.최대값과 최소값을 구할 수 있다.
* */
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
public class 통계학_2108 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int N = Integer.parseInt(br.readLine()); // 수의 갯수 입력(N은 홀수)
int[] arr = new int[N]; // 범위가 [-4000, 4000]인 수를 담을 배열
// 갯수만큼 입력 받기
for(int i=0; i<N; i++){
arr[i] = Integer.parseInt(br.readLine());
}
Arrays.sort(arr);
int max = arr[arr.length-1];
int min = arr[0];
long average = getAverage(arr); // 평균값
int median = getMedian(arr); // 중앙값
int mode = getMode(arr); // 최빈값
int differenceFromMinToMax = max - min; // 범위(최댓값-최솟값)
sb.append(average + "\n");
sb.append(median + "\n");
sb.append(mode + "\n");
sb.append(differenceFromMinToMax + "\n");
System.out.println(sb);
}
// 평균값
private static long getAverage(int[] arr) {
int sum = 0;
int length = arr.length;
for(int i=0; i<length; i++){ // 원소 합 구하기
sum += arr[i];
}
return Math.round((double)sum / length); // 평균값 = 원소의 합 / 원소의 갯수
}
// 중앙 값
private static int getMedian(int[] arr) {
int length = arr.length;
return arr[length / 2]; // 중앙값 = 원소의 갯수 / 2
}
// 최빈값
private static int getMode(int[] arr) {
int[] count = new int[8001]; // count 배열의 인덱스: 값 count 배열의 값: 빈도
int mode = 0; // 최빈 값
// count 배열에 빈도 값 넣기
for(int i=0; i<arr.length; i++){
count[arr[i] + 4000]++;
}
// 다 잊고 배열의 최댓값 찾기 만약 최댓값이 여러 개 일 경우 2번째 순차로 오는 최댓값 찾기
int max =count[0];
boolean flag = false;
// 최대 빈도의 값 구하기
for(int i=0; i<8001; i++){
if(max <= count[i]){
max =count[i];
mode = i-4000; //최대 빈도수가 유일한 경우를 대비해서 먼저 최빈값 구하기
}
}
for(int i=0; i<8001; i++){
if(max == count[i]){
if(flag == false)
flag = true;
else if(flag == true){
mode = i-4000;
break;
}
}
}
return mode;
}
}'Problem Solving' 카테고리의 다른 글
| [자바] 3진법 뒤집기 (0) | 2021.11.11 |
|---|---|
| [코딩테스트] 상위 n개 레코드 (0) | 2021.11.11 |
| [JAVA] 좌표 압축 18870번 (0) | 2021.11.10 |
| [프로그래머스] 이름이 없는 동물의 아이디 (0) | 2021.11.09 |
| [JAVA] 11650번 좌표 정렬하기 (0) | 2021.10.18 |
Comments




