Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- OOP
- 투포인터알고리즘
- 클라우드에서 도커 실행하기
- Spring Web MVC
- MySQL
- 인텔리제이
- java
- Array.asList
- 알고리즘
- 11659
- String.valueOf()
- vm인스턴스생성
- 성능테스트툴
- 코딩테스트
- List.of
- 백준 11659
- 프로그래머스
- 재귀와반복문
- 자바
- Spring MVC 동작원리
- 재귀함수
- Spring MVC 구성요소
- 구간합구하기
- 코드스테이츠 백엔드
- 버블정렬
- GCP
- 백준
- 싱글톤패턴
- 스택
- 코드스테이츠
Archives
- Today
- Total
순간을 기록으로
Java LIS(최대 부분 증가 수열) 본문
문제
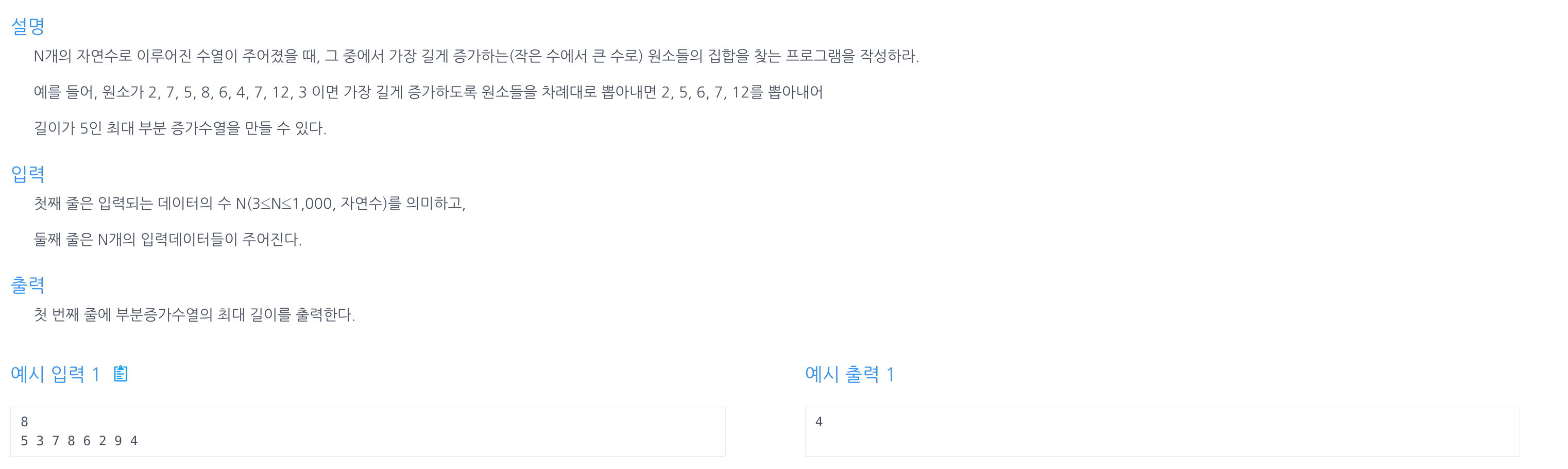
분석
LIS 문제. LIS문제는 dp를 이용해서 풀 수 있다. 이때 dp[i]에 무엇을 저장할 것인지가 중요하다.
dp[i]: i번째 요소를 마지막으로하는 최대 증가 수열의 길이.

dp[0]을 생각해보자. dp[0]은 0번째 요소를 마지막으로하는 최대 증가 수열의 길이를 저장해야 한다. 그러면 직관적으로 1이라는 것을 알 수 있다. dp[0]은 항상 1이기 때문에 초기화를 해줘야 한다.
dp[1]은 1번째 요소를 마지막으로하는 최대 증가 수열의 길이를 저장해야한다. arr[0]이 5이고, arr[1]이 3이므로 최대로 만들 수 있는 길이는 1이다.
dp2[]는 2번째 요소를 마지막으로하는 최대 증가 수열의 길이를 저장해야 한다. {5,7}, {3,7}이 있으므로 dp[2]는 2가 된다. 이런식으로 구하면 arr과 dp는 다음과 같이 되고 LIS의 길이는 4가 된다.
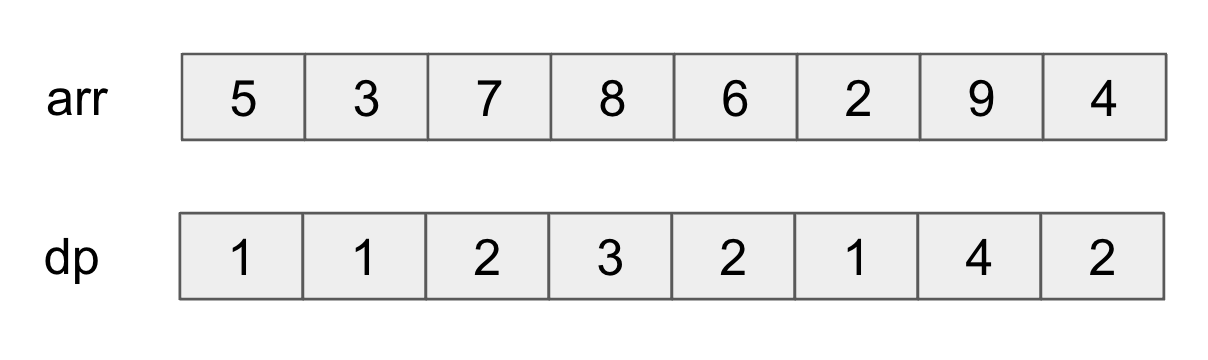
핵심은 dp 요소값을 구할 수 있느냐다.
dp[i]를 구하는 로직을 일반화하면 아래와 같다.
- dp[0]은 구했으니 for 1<=i<arr.len 반복
- 최대값을 저장할 max 선언
- for(0<=j<i)
- 앞 부분 값들 중에서 현재 값보다 작고, dp[j]> max 이면 max = dp[j]
- dp[i] = max + 1
소스코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class 최대부분증가수열 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
int answer = 1;
int[] dp = new int[arr.length];
dp[0] = 1;
for (int i=1; i<arr.length; i++) {
int max = 0;
for (int j=0; j<i; j++) {
if (arr[j] < arr[i] && dp[j] > max) max = dp[j];
}
dp[i] = max + 1;
answer = Math.max(answer, dp[i]);
}
System.out.println(answer);
}
}'Problem Solving' 카테고리의 다른 글
| [Java] 백준_신기한 소수_2023 (0) | 2022.08.17 |
|---|---|
| [Java] 백준_연결 요소의 개수_11724 (0) | 2022.08.17 |
| [Java] 백준_좋다_1253 (0) | 2022.08.10 |
| [Java] 백준_수들의합5_2018 (0) | 2022.08.09 |
| [Java] 백준_구간합구하기_11659 (0) | 2022.08.05 |
Comments




